Margin of error calculations are an essential part of any survey results. Even if you’ve never conducted a survey before, you’ve likely seen the margin of error expressed as a plus-minus sign. In simple terms, it shows how much variance there may be when comparing the survey results to how things may actually be.
What is Margin of Error?
Margin of error (MoE) is a statistical concept that attempts to derive the uncertainty and amount of error in a survey. The margin of error is usually expressed as a plus-minus sign with percentage points (e.g., ±4%), which is read as variance in results.
For example, if 50% of consumers prefer some product, a margin of error of ±4% means that the true preference can vary between 46% to 54%. Margin of error calculations are dependent on several factors, each of which can influence how close to reality your results may be.
How To Calculate Margin of Error
All margin of error calculations require three metrics—population size, confidence level, and sample size. These three metrics each influence the margin of error in their own unique way.
- Population size. The total (potential) number of people your survey or study is supposed to represent. In other words, it’s the pool from which you will be collecting your sample. Population size may be the total number of citizens in a country, the population of a city, or the number of customers a business serves.
- Confidence level. It represents the long-term performance of your survey results. Industry-standard confidence level is set at 95% or 99%. In simple terms, confidence level means that if you were to repeat the study infinitely many times, 95% of those studies would contain the true population mean.
- Sample size. The real number of people that have participated in your survey. In other words, that’s the survey data you have.
Before we explain how to calculate margin of error, there’s a few more important aspects to these three metrics.
Population size will largely remain static as long as you’re conducting surveys about the same topic. While the amount of customers or citizens may actually change fairly frequently, the population is usually a large enough number that you don’t have to account for minor changes.
As populations increase, however, so should your sample size. There are limits to it, but generally larger sample sizes represent populations better due to the Law of Large Numbers. Yet, it also highly depends on the confidence level.
Confidence level determines, as mentioned, how accurate your study data is. Sample size, on the other hand, determines how close your study results are to the real population mean. That means that if you want a higher confidence level, you need a larger sample size.
The exact mathematical relationship between confidence level and sample size is quite complicated, so it’s enough to know that they’re related to each other.
So, with all three metrics at hand, you can start calculating the margin of error. There are two ways to go about it.
Margin of error can be calculated for estimating a proportion (such as how many people prefer a product, policy or behavior). You can do so with the margin of error formula below:
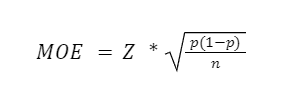
Z – the Z-score for your selected confidence level. See table below for Z-scores for the most popular confidence level estimates.
p – sample proportion. You get the sample proportion by dividing the number of positive (or negative) responses by the total number of responses in your survey results.
n – the sample size.
If you’re estimating a mean (such as average age, income, etc.), you’ll have to use a different margin of error formula:
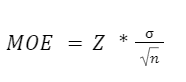
Z and n remain the same – the Z-score and the sample size. Sigma (σ) is the standard deviation of the population. If one is not available, the standard deviation of your survey data is often used as an estimation.
Finally, you can always find a margin of error calculator online where you’ll only have to plug in your data. Some of them may also come with additional features such as sample size calculation. However, you may have to find a margin of error calculator that suits your needs as some will only work for proportions and others only for means.
How to Reduce Margin of Error
If you’ve played around with a margin of error calculator, you’ve likely already noticed several ways to reduce your survey’s margin of error. A few of them, however, may only be possible in specific cases.
1. Increase sample size
Increasing your sample size is the most straightforward way to reduce margin of error. The margin of error is inversely proportional to sample size, however, which has a twofold effect. If your starting sample size is relatively small, then even minor increases can greatly affect your margin of error.
However, the opposite is also true. Making improvements to margin of error when you already have a large sample size will be significantly more difficult as you’ll need to add a lot of respondents to move the needle.
So, increasing sample size is most effective if you started out small. Otherwise, resource constraints will likely make the method less viable than others.
2. Decrease confidence level
Another obvious method is to decrease the confidence level. Decreasing it means you’ll need a smaller sample size to get the same margin of error. If you maintain the same one, but decrease the confidence level, then you’ll reduce the margin of error as well.
Unfortunately, that also has a major drawback—your study results become less reliable and accurate as confidence level decreases. So, while your margin of error may be lower, so is the likelihood of the accuracy of your results.
3. Reduce variability (only applicable to means)
If the survey is measuring means (e.g., income, age, height, etc.), you can rework your sample to reduce variability in results.
For example, a more homogenous sample (in some other metric such as household ownership) can be chosen, however, it may affect the possible conclusions of the survey.
Another way to reduce variability would be to review survey questions to remove or modify those that have room for interpretation.
4. Finite Population Correction (FPC)
Another method that’s somewhat restricted, FPC is usually used when your sample size is 5% or more of the entire population. The underlying mechanism of how FPC works can be complicated, but can be partly explained by an analogy.
When you have a standard deck of playing cards (52 cards in total), the likelihood of drawing a card of any suit is evenly distributed (13/52 for each suit). If you draw 4 hearts out of the deck (48 cards remaining), the likelihood of drawing the remaining three suits at random increases (13/48) while the likelihood of drawing hearts decreases (8/48).
Finite Population Correction works in a similar fashion—if your population is not infinite, each respondent in your survey reduces the number of unknowns in the population. Once you reach 5% of the population in your sample size, the effects start becoming increasingly pronounced.
For example, if you were to survey 75% of the population, the likelihood that the remaining 25% would completely flip the results is extremely small. Adjusting for FPC would also significantly decrease the margin of error for your results.
Conclusion
Margin of error is a foundational part of surveys. While it’s inevitable and unavoidable, there are numerous ways to reduce it by tinkering with your survey and sample. There are many other ways to reduce margin of error, however, such as using weighting techniques or using different sampling methods.


